Un verre d’eau est posé sur un plateau qui peut tourner comme une fronde grâce à quatre ficelles tenues à bout de bras.Lorsque le verre à la tête en bas, que va faire l’eau contenue dedans ?
Fiche d’accompagnement de l’expérience:
Matériel
-
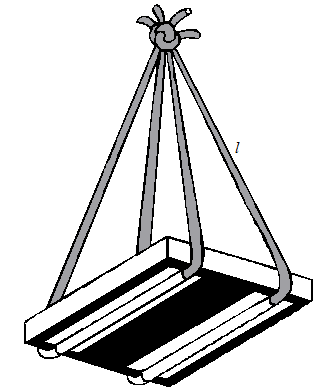
une planche de bois (dimensions approximatives : 20 cm x 20 cm x 1 cm)
-
2 ficelles identiques (longueur : environ 3 m)
-
du ruban adhésif
-
une tasse avec de l’eau
Montage et réalisationBien fixer les deux ficelles sous la planche à l’aide de ruban adhésif (la figure précédente représente le dispositif vu de dessous).
Nouer les 4 bouts de telle sorte que les longueurs l des ficelles soient égales.
Poser une tasse d’eau sur le plateau.
Tenir le plateau par le nœud : on peut le faire osciller dans tous les sens sans que la tasse ne glisse ni que l’eau ne déborde, à condition que les ficelles restent tendues et en prenant soin d’éviter que le plateau percute un obstacle ou qu’il s’accroche quelque part.
Avec un peu d’audace, on peut lui faire faire un tour complet (« soleil »).
Les oscillations d’amplitude a comprise entre 90° et 180° sont interdites car la tasse glisse si l’élongation du point de rebroussement est supérieure à 90°.
Une élongation supérieure à 90° n’est possible que s’il s’agit d’un tour complet avec une vitesse suffisante.
ExplicationsLorsque le plateau décrit une portion de trajectoire circulaire centrée sur C comme sur la figure ci-dessous, le plateau et la tasse ont une accélération. Pour que le schéma reste lisible, nous n’avons représenté que l’accélération de la tasse.
Dans le référentiel de la tasse (non galiléen), celle-ci est soumise à l’accélération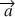 
qui est la somme de l’accélération de la pesanteur 
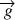et de l’accélération centrifuge 
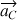. Notons 
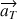la composante tangentielle de l’accélération et 
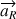sa composante radiale. On voit sur la figure que 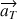est égale à la composante tangentielle de 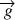, alors que 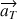est égale à la somme de l’accélération centrifuge 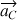et de la composante radiale de 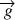. Notons 
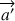l’accélération du plateau. L’accélération radiale du plateau est différente de celle de la tasse (car leurs distances au centre du cercle C sont différentes et non pas, comme on pourrait le croire, parce que leurs masses sont différentes). L’accélération tangentielle du plateau 
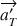est identique à celle de la tasse ( 
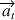) car elle est égale à la composante tangentielle de 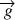. La tasse ne glisse donc pas par rapport au plateau car les deux objets ont des accélérations tangentielles identiques. C’est pour la même raison que l’eau ne s’échappe pas de la tasse (même accélération tangentielle pour la tasse et pour l’eau). La tasse peut glisser si le plateau vient percuter un obstacle ou bien s’il reste accroché, car le plateau est alors soumis à une force supplémentaire et son accélération tangentielle devient différente de celle de la tasse. Il faut une certaine force de frottement entre le plateau et la tasse pour que la tasse soit entraînée par le plateau au début du mouvement.
Examinons plus précisément ce qui se passe lors d’un tour complet à la vitesse angulaire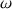 
, supposée constante, toujours dans le référentiel de la tasse. Sur la figure suivante, on a représenté l’accélération centrifuge 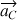(flèche fine), l’accélération de la pesanteur 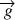(flèche moyenne) et la composante radiale 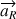(flèche épaisse) de l’accélération totale pour différentes valeurs de l’angle a.
Le centre de gravité du système se déplace sur la ligne pleine. La ligne pointillée correspond à l’extrémité de la flèche représentant l’accélération centrifuge (de valeur constante puisqu’on a supposé w constante). Il s’agit de la valeur la plus faible de la vitesse angulaire pour laquelle on peut réaliser un tour complet sans que tout tombe. Dans la position la plus haute (a = 180°), l’accélération centrifuge compense tout juste 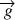. On en déduit la vitesse de rotation minimale pour pouvoir faire un tour complet sans s’éclabousser :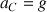
donc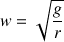 
Notons f la fréquence minimale avec laquelle on doit tourner le bras pour que tout tienne :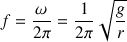
Avec
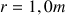
et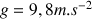 
,
on calcule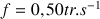 
.
La 2 ème figure montre ce qui arrive si le point de rebroussement des oscillations se trouve dans la zone interdite (90° < a < 180°) : au point de rebroussement,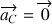 
et donc 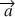se ramène à 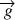, entraînant ainsi la chute du plateau, du verre et de l’eau (c’est sans conséquences fâcheuses tant qu’ils sont en chute libre, mais les problèmes apparaissent lorsqu’ils arrivent sur le sol…).
RemarquesLa manipulation de ce plateau centrifuge demande une certaine habileté, même pour les mouvements autorisés par les lois de la physique.
En premier lieu, il faut se placer loin de toutes les sources potentielles de chocs : tables, chaises, murs, etc., sans oublier l’expérimentateur (un choc contre ses jambes met l’expérience en péril, mouille son pantalon et peut même le blesser).
Vous devrez vous exercer car on ne peut pas faire le tour complet en augmentant progressivement l’amplitude des oscillations : n’oubliez pas qu’il faut « sauter » la zone interdite (90° < a < 180°) et accompagner le mouvement après le tour complet en baissant le centre C du cercle.
On peut considérer cette expérience-ci comme encore plus difficile que celle qui consiste à faire faire des tours complets à un panier à salade ou à un seau d’eau (car la main ne retient pas la tasse sur le plateau).
Le principe du plateau centrifuge est utilisé pour la suspension des étagères des bateaux. On raconte aussi qu’un astronome amateur anglais a présenté ce dispositif ingénieux à la télévision. Ce plateau lui permet de monter sa tasse de thé dans l’escalier en colimaçon qui mène à son observatoire sans en renverser une seule goutte.
Le plateau fabriqué ici peut être réutilisé pour l’expérience « La force de Coriolis ».